Amateur Theory of Disc Golf Physics

Joseph DeVictoria March 2022

Intro:

In this article I am going to attempt to many of the important physics that come into play while throwing golf discs.

I will start off with the disclaimer that I am not a physicist and I haven't done any controlled experiments to prove what I'm about to say, but I hope to bring focus to the most fundamental concepts of disc sports.

This shouldn't be too technical hopefully anyone who took physics in high school will be able to follow along.

Now if you have been playing disc golf, watching disc golf on youtube, or spending time with disc golfers, you have probably heard phrases like these:

• "I don't have the arm speed for that disc."
• "It hyzered out on me."
• "Anthony Barela can make a destroyer turn over and roll."
• "I've been seasoning that disc for a while. Now that its beat in, it flies very understable."
• "Base plastics are flippier."
• "Base plastics beat in faster."

etc...

Everyone seems to intuitively understand some of these statements, but their reasoning is hard to explain. Let's start with some context.

Context:

When considering the flight of a modern disc golf disc, most new players today are thrown into the ring with the Innova Flight rating system that has been generally adopted by all disc golf manufacturers.

This system characterizes the relative speed, glide, turn, and fade of a golf disc in flight. I think there are many words and phrases on this diagram which are imprecise and ambiguous, such as "power".

If you are reading this article, hopefully you are already somewhat familiar with what each one of these numbers represents. If not, there are a lot of excellent articles, reddit posts, and YouTube videos which explain this concept based on Innova's original description.

I would like to do my own brief practical summary of what I have learned about these numbers to help start the context for the discussion:

Speed represents the aerodynamic profile of a golf disc - that is to say how much drag the disc will experience from air resistance as it moves parallel to the earth during flight. This number gets larger as the disc gets "faster" or more aerodynamically efficient. More aerodynamic efficiency generally correlates with the sharpness of the wing and the overall thickness of the disc when viewed from its profile. Slow discs tend to be tall with blunt noses while fast discs tend to be very flat with sharp tapered noses. In order to flatten a disc, we also typically see more of the mass of the disc moved to the edge of the disc which gives high speed drivers their characteristic "wide rim". Even though fast discs can help in generating more distance under the right conditions and skill, slow discs are also a powerful tool since controlling distance is just as important as being able to throw far in disc golf.

Glide represents the amount of lift and/or parachute action your disc will generate during flight. While spinning, discs acts as a wing or foil in the air - similar to an airplane wing. Discs that have wing shapes that generate lift from forward motion, or do a good job of "parachuting" as they slow down will have a higher glide rating. This is why some slow discs can have the same or even higher glide rating than a high speed disc. You can intuitively feel this when you throw a glidey disc low and flat, yet somehow it glides farther than you could ever dream of a ball doing on the same line. This is the namesake of the classic documentary The Invisible String. Discs with a low glide rating often rely heavily on a slightly elevated nose angle to fly, since they are not easily able to translate forward motion into sustained flight.

Turn represents the propensity of the disc to turn or slide towards its spin direction during flight. This number is the only one that is measured typically in negative numbers, since it represents the discs travelling in the opposite direction of the fade which we will talk about next. In my opinion, this is the most mysterious number in the flight system since it relies heavily on the geometry of the disc, the angle of attack, and the amount of spin on the disc - which can be very difficult for newer players to understand intuitively. I will focus heavily on this number in this article.

Fade represents the disc's behavior at the end of its flight - when the disc has expended its forward momentum or its angular (rotational) momentum. This fade is typically that dumpy drop towards the opposite direction of the spin. Discs with a large amount of fade will (for many possible reasons) fight towards the opposite direction of spin, which can become pronounced and even knife-like as the disc flies, especially as it slows. "Overstable" discs generally have high speed overstability (think destroyer, boss), low speed overstability (think pig or gator), or both (think firebird). I make a distinction between the two because of the way they fly and how they fade. Something like a champion plastic firebird will typically move left (RHBH) during most of its flight, while something like a Pig may flight straight for 85% of its flight and only dump hard at the end as it slows down. Discs with low fade will tend to finish flat, or with a soft dump. I will touch on this number heavily in this article as well.

Physics

Now that we have that out of the way, I want to start diving into a couple physics concepts that are very valuable to understand if you want to figure out why a disc flies the way it does. I will even offer my theories on why a disc turns more as it wears in and becomes seasoned from use.

Based on my research and understanding, I suggest that there are two fundamental physical mechanics involved in the motion of discs in flight, and I will do my best to explain them in order of importance:

Gyroscopic Effect

The first is called the gyroscopic effect. This effect can be generalized as the tendency of a rotating object to resist changes in orientation. Most if not all of you have either had a lesson in physics class or an experience while playing with your bicycle where you hold the axle of a rotating wheel and noticed some of the non-intuitive features of gyroscopic physics. Perhaps the most notable thing you would feel is the powerful counteractive force that the wheel exerts against you when you try to twist or tilt the axle away from the axis of rotation.

The reason this reactive force feels strange is that its not quite the same as something like shooting a rifle or hitting a baseball, where the resultant force vectors are mostly linear. (i.e. you feel a rifle press back hard against your shoulder as the relatively small bullet is projected out the front of the weapon at tremendous velocity) The reactive forces you feel from a spinning object behave in accordance with a vector of angular momentum instead of linear momentum.

Whereas the vector of linear momentum is basically just a straight line (barring the interaction with other forces during its motion) the vector of angular momentum lies along the "axle" for lack of a better term of the spinning object. This vector follows the right hand rule that you may have heard of in high school or college physics. Basically as you take your right hand and curve your fingers along the direction of rotation - you can extend your thumb and it will point in the direction of the vector which represents the angular momentum. If you change the direction of rotation, the vector points in the opposite direction, which we will cover as we apply this to discs.

Now this vector has both a direction and a magnitude as you might remember from despicable me. The direction is found using the right hand rule, but the magnitude of the angular momentum basically depends on the angular velocity and the moment of inertia of the object. Moment of inertia could probably cover an entire YouTube video by itself, but lets just make it simple and say that it is basically a measurement of how far an object's mass is located from the center. The farther out you can put the weight, the greater the moment of inertia is.

Intuitively, objects which have a large moment of inertia, who have their weight distributed far away from their center are far harder to get spinning than those with their weight towards the center. Think of an ice skater who pulls their arms and legs in tight as they spin so that they can spin faster, and immediately slow their spin by extending. You have probably experienced this on the playground as a kid if you were lucky enough to have a red-blooded tire swing at your park. Leaning out from the swing causes you to spin slowly, but as you pull your weight to the middle angular velocity becomes easier and easier. (This is actually called the conservation of inertia) Its the same reason why you can generate far more violent impacts from a hammer whos' head is at the very end of the shaft than one with a head mounted right next to your hand - its harder to swing, but it has more inertia.

Getting back to discs - you have to think of that angular momentum as a product of your disc's weight and geomerty, but largely as a factor of its angular velocity. Angular velocity is SPIN! - rotations per second, radians per second, whatever unit of measurement you want to use, its the SPIN. I really want to emphasize this, because what it means is that regardless of your particular disc, its propensity to resist motion in any direction is directly proportional to how fast it is spinning. There is another effect of spin which I will go into later that affects your disc's flight, but for now just know that when throwing a disc - the moment it leaves your hand, you have started it out with a decaying quantity of angular momentum as well as linear momentum. Why is it decaying? Well because the spin is being slowed by surface friction with the air all around the disc. And the forward velocity is being slowed by the drag it experiences from the air. Each rotation skims a little bit of angular speed from the disc similar to if you were applying friction to the top of a record with your finger. If you were to set a disc spinning in deep outer space, it would just keep going until some other force acted upon it.

The next question is then, if a spinning disc resists movement, then why does a disc turn and fade?

To understand the turn of a disc, we need to look at how new torques which are not along the axis of rotation affect its flight and orientation. We talked previously about the right hand rule, and how an applied torque and its resultant angular velocity generates an angular momentum vector along the "thumb" axis. Well this same right hand rule applies to other forms of torque which could apply themselves to the disc. For a disc in flight, this mainly comes from pressure and friction created from the drag of the air.

Let us consider a fairly standard disc golf fairway driver. Let's use my favorite Innova mold, the Teebird3 as an example for modeling the forces at play during flight.

If we say that the disc is flying from left to right, then we should imagine the are we are receiving air resistance which applies a force in the opposite direction. As the air travels around the disc, it creates areas of higher and lower than atmospheric pressure similar to a air foil or wing. I'm not going to go terribly in depth on the concept of lift and the miracle of flight, but just remember that you do get some lift from certain disc shapes. in this example, the air is going to be applying downward pressure along the top of the disc and some upward pressure from the edge of the bottom of the disc. These pressures create a force on the disc which turns into a rotational torque since there is no equivalent pressure being generated at the back edge of the disc. Where there is rotational torque, a new vector of angular momentum is created which follows the right hand rule again.

Bear with me here, because this is the grittiest and hardest part of the article to explain and understand:

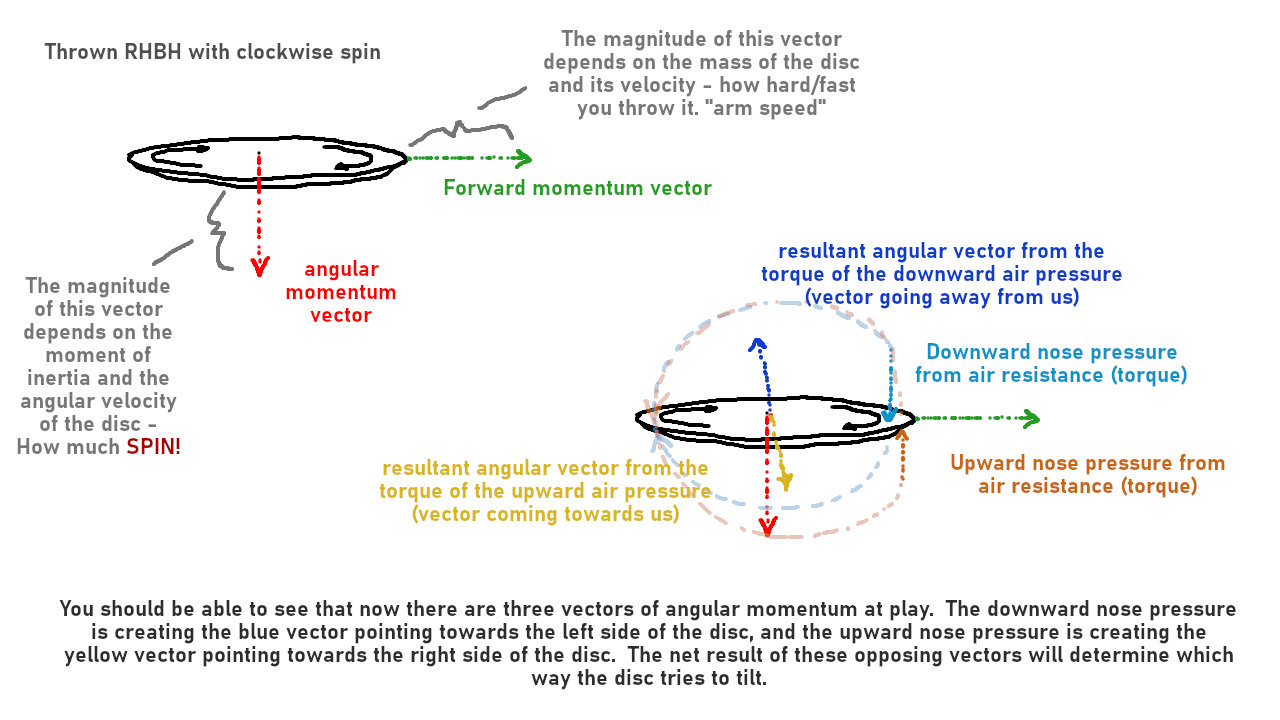
With gyroscopic motion, all the vectors of angular momentum being applied to the disc will try to cancel out. This means that they will move towards each other until equilibrium is established and the disc no longer needs to change its orientation. This equation is constantly changing during a throw since the angular and forward velocities will change constantly throughout the disc's flight.

For our example here, depending on the magnitude of the angular momentum created by the upward and downward nose pressure, you will end up with some net nose-pressure-induced angular momentum which will try to cancel the original angular momentum created by the spin of the disc. The movement of these vectors causes the disc itself to tilt which alters the trajectory of its flight, making it "turn" or "fade". In this example, since we are assuming clockwise RHBH spin:

• If downward nose pressure comes out dominant, the disc will begin to tilt to the right since the original downward vector is chasing the new vector pointing left. ("understable flight")
• If downward and upward nose pressure are equivalent, then the yellow and blue vectors cancel out entirely and the disc just flies on whichever angle you released it until the forward and angular momentum changes.
• If upward nose pressure comes out dominant, the disc will begin to tilt to the left since the downward vector is chasing the new vector pointing right. ("overstable flight")

The physical shape of the disc (especially the rim) drastically affect the distribution of this nose pressure, leading to discs which are inherently more overstable or understable. Experienced disc golfers can often pick up a disc and infer its stability simply from feeling the rim. Why? Because they associate steeply slanted bottom rims with overstable flight and high rounded upper rims with understable flight. You may get something in the middle which is hard to peg, but generally they will guess correctly.

Now what about when I throw the disc and it doesn't actually turn or tilt at all, but it does seem to "slide" laterally during its flight??

This phenomenon is called the Magnus effect.

Magnus Effect

We can learn most of what we need about this from the wikipedia entry:

"The magnus effect is an observable phenomenon commonly associated with a spinning object moving through a fluid. The path of the spinning object is deflected in a manner not present when the object is not spinning. ... The most readily observable case of the Magnus effect is when a spinning sphere (or cylinder) curves away from the arc it would follow if it were not spinning. ... It is often used by association football and volleyball players, baseball pitchers, and cricket bowlers. Consequently, the phenomenon is important in the study of the physics of many ball sports. ... Topspin in ball games is defined as spin about a horizontal axis perpendicular to the direction of travel that moves the top surface of the ball in the direction of travel. Under the Magnus effect, topspin produces a downward swerve of a moving ball, greater than would be produced by gravity alone. Backspin produces an upwards force that prolongs the flight of a moving ball. Likewise side-spin causes swerve to either side as seen during some baseball pitches, e.g. slider. The overall behavior is similar to that around an aero foil (see lift force), but with a circulation generated by mechanical rotation rather than shape of the foil.

The deflection can be explained by the difference in pressure of the fluid on opposite sides of the spinning object. The Magnus effect is dependent on the speed of rotation." (Wikipedia)

That backspin behavior is what allows airsoft BBs to fly drastically farther than they could out of a simple tube. That's called hop-up in airsoft, but if you play baseball this is what goes into a fastball pitch. This type of pitch can often fool batters since they may think it is flying faster than it is due to how little perceived drop there is in its flight. They may miss early, or low since they expect more drop from a flying object.

Though frequently associated with ball based sports, the magnus effect is alive and well in disc sports too. As a disc spins through the air the plastic surface of the disc interacts with the air around it via friction. This friction can actually propel air at a relatively higher velocity towards the direction of the spin. When this happens, if the pressure difference is great enough (being generated by enough spin, or an object which has a high enough coefficient of friction with the air) then the disc will actually slide or drift towards the direction of the spin. For the example of a RHBH throw, the disc "slides" to the right instead of "turning" to the right. Regardless of how you throw it, RHFH, LFBH, LHFH - the slide will always be in the direction of the spin at the nose.

This begs the question, will discs which have more friction with the air exhibit more of the magnus effect in flight? I would suggest that this is definitely the case. This also gives credence to the notions that base plastics which are often coarse, rough, grippy, and easy to scratch and scuff are more "flippy/understable/etc." than premium plastics which are slick, firm and do not scratch, scuff, or deform easily over time. As plastics get more scratches, nicks, dings, and scuffs, they exert more friction on the air leading to more slide from magnus effect. Premium plastics do this slower because of how hard the plastic is, but I've observed they also seem to increase their friction as hand oils build up on the rim. This is definitely not the only factor in discs "beating in", and I also have some theories about the deformation of plastic in flight which would further explain differences in stability between base plastics and premium plastics, but I'm not going to go into it in this article. Either way hopefully the description is clear and you can carry out this thought experiment in your head with your own experiences to recognize the magnus effect in your throwing. You can abuse the Magnus effect by utilizing discs with a coarse surface such as base plastics throwers, or by adding more spin to your disc.

Summary

Throwing golf discs accurately at distance requires a careful mental and physical balancing of the gyroscopic effect, magnus effect, velocity and disc selection. Understanding how spin, nose angle, and disc selection affect disc turn in flight will help you begin to develop shots in your bag which get you lower scores on the course. I think experienced players can intuitively grasp all the discussion points from this article, but attaching these intuitive discoveries to documented physical behavior will help us understand better.

Some parting tips I have for people looking to apply these concepts and get better:

1. When in doubt, you should probably just add more spin. Fast spin tempers the disc's propensity to tilt off axis (both turn and fade) and will help you throw straight. It also works with any speed of disc. (putters -> drivers)
2. Throwing a good shot is really about managing several connected variables: the forward velocity, spin, disc selection, angle of attack, and release angle. To learn how these variables affect flight, try throwing a single disc and maintain as many of these variables constant as you can while trying to change a single one to experiment. (such as spin or attack angle) You should start to intuitively see patterns of which variables cause the disc to turn over or slide. Combining them all correctly is what you see the pros on Jomez doing.
3. Big distance requires big spin. If a disc loses its angular momentum, it doesn't matter how fast it was moving through the air, it will start to fall and fade. This behavior is usually seen when beginners throw big-rim drivers and they are getting massive flare skips at the end of their flight - they probably threw it with enough forward momentum for it to keep moving, but not enough angular momentum for it to keep spinning. (and hence flying) This is one of the biggest secret sauces of players like Drew Gibson, Garret Gurthie, and Anthony Barela - sure they throw fast discs, have very high release velocities, but they also have extremely high RPM. (snap / spin)

I look forward to reading your comments!